Jadual Trigonometri Sin Cos Tan Lengkap (Semua Sudut) + Cara Memahaminya

The trigonometric table sin cos tan adalah rangkaian jadual yang mengandungi nilai trigonometri atau sin cos tangen suatu sudut.

Dalam artikel ini, jadual nilai trigonometri untuk sin cos tan ditunjukkan dari pelbagai sudut khas dari sudut 0º hingga 360º (atau yang biasa disebut sudut bulatan 360 darjah), sehingga anda tidak perlu repot menghafalnya lagi.

Mengenai formula identiti trigonometri, anda boleh membacanya dalam artikel ini.

Definisi Sin Cos Tan

Sebelum memasuki jadual nilai trigonometri, ada baiknya kita memahami terlebih dahulu istilah trigonometri dan sin cos tan.

• Trigonometri adalah cabang matematik yang mengkaji hubungan antara panjang dan sudut segitiga.
• Sin (sinus) adalah nisbah panjang dalam segitiga antara depan sudut dan hipotenus, y / z.
• Cos (cosine) adalah nisbah panjang dalam segitiga antara sisi sudut dan hipotenus, x / z.
• Tan (tangen) adalah nisbah panjang dalam segitiga antara depan sudut dan sisi, y / x.

Semua perbandingan trigonometri tan sin cos hanya terhad kepada segitiga atau segitiga kanan yang sah dengan satu sudut 90 darjah.

Jadual Trigonometri Sudut Khas Kuadran I (0 - 90 darjah)

Sudut	0 º	30 º	45 º	60 º	90 º
Dosa	0	1/2	1/2 √2	1/2 √3	1
Cos	1	1/2 √3	1/2 √2	1/2	0
Tan	0	1/2 √3	1	√3	∞

Jadual Trigonometri Sudut Kuadran II Khas (90 - 180 darjah)

Sudut	90 º	120 º	135 º	150 º	180 º
Dosa	1	1/2 √3	1/2 √2	1/2	0
Cos	0	- 1/2	- 1/2 √2	- 1/2 √3	-1
Tan	∞	-√3	-1	- 1/3 √3	0

Kuadran Sudut Khas Meja Sin Cos Tan III (180 - 270 darjah)

Sudut	180 º	210 º	225 º	240 º	270 º
Dosa	0	- 1/2	- 1/2 √2	- 1 / 2√3	-1
Cos	-1	- 1 / 2√3	- 1 / 2√2	- 1/2	0
Tan	0	1 / 3√3	1	√3	∞

Kuadran Sudut Khas Meja Cos Sin Tan IV (270 - 360 darjah)

Sudut	270 º	300 º	315 º	330 º	360 º
Dosa	-1	-½√3	-½√2	-½	0
Cos	0	½	½√2	½√3	1
Tan	∞	-√3	-1	-1 / 3√3	0

Demikianlah senarai jadual trigonometri yang lengkap dari semua sudut khas dari 0 - 360 darjah.

Baca juga: Proses Mekanisme Penglihatan Manusia dan Petua Penjagaan Mata

Anda boleh menggunakan jadual ini untuk memudahkan perniagaan dalam mengira atau menganalisis trigonometri dalam matematik.

Mengingat Jadual Trigonometri Sudut Khas Tanpa Menghafal

Sebenarnya, anda tidak perlu bersusah payah menghafal semua nilai trigonometri dari setiap sudut.

Yang anda perlukan adalah konsep pemahaman asas yang boleh anda gunakan untuk mencari nilai trig dari sudut tertentu.

Anda hanya perlu mengingati komponen panjang sisi segitiga pada sudut khas 0, 30, 45, 60, dan 90 darjah.

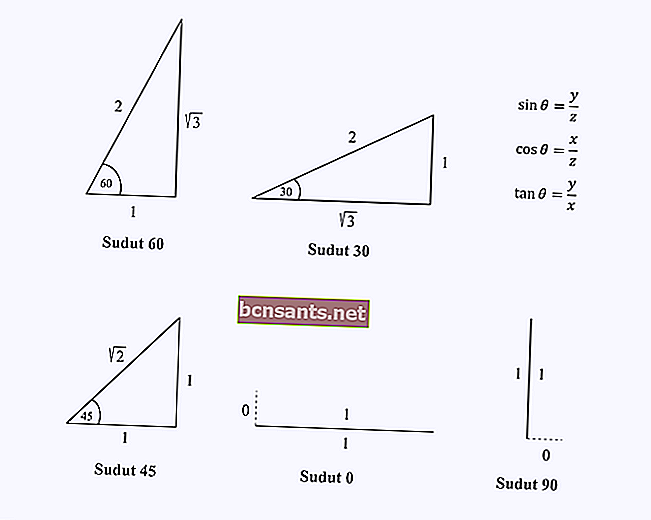
Katakan anda ingin mencari nilai kos (60).

Anda hanya perlu mengingat panjang sisi segitiga dengan sudut 60 darjah, kemudian lakukan operasi kosinus, yang x / z pada segitiga itu.

Dari rajah tersebut, anda akan melihat bahawa nilai untuk cos 60 = 1/2.

Mudah kan?

Untuk sudut pada kuadran lain, kaedahnya sama dan anda hanya perlu menyesuaikan tanda positif atau negatif setiap kuadran.

Jadual Dalam Bentuk Bulatan

Sekiranya jadual cos sin tan di atas terlalu panjang untuk diingat, juga jika kaedah konsep sudut khas yang anda fikirkan masih sukar ...

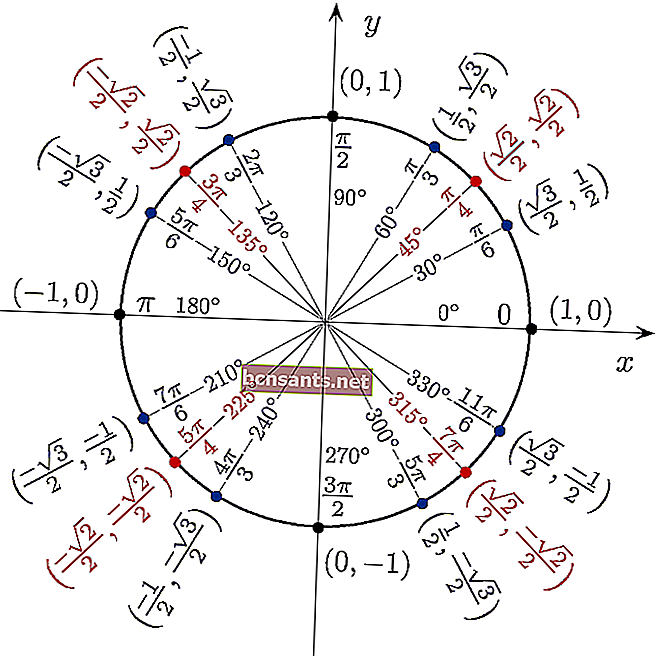
Anda boleh menggunakan jadual trigonometri dalam bentuk bulatan untuk melihat secara langsung nilai sin cos tan dari sudut 360 darjah.

Trik Pantas untuk Menghafal Jadual Trigonometri

Sebagai tambahan kepada kaedah di atas, ada satu kaedah lagi yang boleh anda gunakan untuk mengingat jadual formula trigonometri dengan mudah.

Langkah-langkah yang perlu anda lakukan adalah seperti berikut:

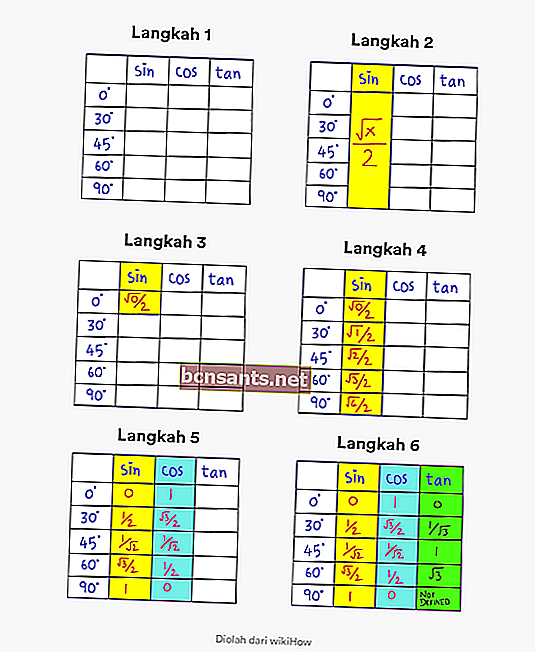
• Langkah 1 . Buat jadual yang mengandungi sudut 0 - 90 darjah dan lajur dengan keterangan sin cos tan
• Langkah 2 . Perhatikan bahawa formula umum untuk dosa pada sudut 0 - 90 darjah ialah √x / 2.
• Langkah 3 . Tukar nilai x ke 0 pada √x / 2 pada lajur pertama. Sudut kiri atas.
• Langkah 4. Isi mengikut urutan dengan menukar x menjadi 0, 1, 2, 3, 4 di lajur sin. Oleh itu, anda telah mendapat dosa nilai trigonometri yang lengkap
• Langkah 5 . Untuk mencari nilai kos, semua yang perlu anda lakukan ialah membalikkan susunan di ruang sin.
• Langkah 6 . Untuk mencari nilai tan, yang perlu anda lakukan ialah membahagikan nilai sin dengan nilai kos.

Baca juga: Cerita Fiksyen: Contoh, Definisi dan Unsur [PENUH

Mana yang lebih mudah untuk anda fahami untuk mengingat nilai trig dari tan sin cos?

Mana tidaknya, pilih yang paling mudah untuk anda fahami. Kerana setiap orang mempunyai gaya pembelajaran yang berbeza.

Jadual Untuk Semua Sudut

Sekiranya dalam jadual di atas nilai yang ditunjukkan hanyalah nilai trigonometri sudut khas, maka jadual ini menunjukkan semua nilai trigonometri semua sudut dari 0 - 90 darjah.

Sudut	Orang radian	Dosa	Cos	Tan
0 °	0	0	1	0
1 °	0.01746	0.01746	0.99985	0.01746
2 °	0.03492	0.03491	0.99939	0.03494
3 °	0.05238	0.05236	0.99863	0.05243
4 °	0.06984	0.06979	0.99756	0.06996
5 °	0.0873	0.08719	0.99619	0.08752
6 °	0.10476	0.10457	0.99452	0.10515
7 °	0.12222	0.12192	0.99254	0.12283
8 °	0.13968	0.13923	0.99026	0.1406
9 °	0.15714	0.1565	0.98768	0.15845
10 °	0.1746	0.17372	0.9848	0.1764
11 °	0.19206	0.19089	0.98161	0.19446
12 °	0.20952	0.20799	0.97813	0.21265
13 °	0.22698	0.22504	0.97435	0.23096
14 °	0.24444	0.24202	0.97027	0.24943
15 °	0.26191	0.25892	0.9659	0.26806
16 °	0.27937	0.27575	0.96123	0.28687
17 °	0.29683	0.29249	0.95627	0.30586
18 °	0.31429	0.30914	0.95102	0.32506
19 °	0.33175	0.32569	0.94548	0.34448
20 °	0.34921	0.34215	0.93965	0.36413
21 °	0.36667	0.35851	0.93353	0.38403
22 °	0.38413	0.37475	0.92713	0.40421
23 °	0.40159	0.39088	0.92044	0.42467
24 °	0.41905	0.40689	0.91348	0.44543
25 °	0.43651	0.42278	0.90623	0.46652
26 °	0.45397	0.43854	0.89871	0.48796
27 °	0.47143	0.45416	0.89092	0.50976
28 °	0.48889	0.46965	0.88286	0.53196
29 °	0.50635	0.48499	0.87452	0.55458
30 °	0.52381	0.50018	0.86592	0.57763
31 °	0.54127	0.51523	0.85706	0.60116
32 °	0.55873	0.53011	0.84793	0.62518
33 °	0.57619	0.54483	0.83854	0.64974
34 °	0.59365	0.55939	0.8289	0.67486
35 °	0.61111	0.57378	0.81901	0.70057
36 °	0.62857	0.58799	0.80887	0.72693
37 °	0.64603	0.60202	0.79848	0.75396
38 °	0.66349	0.61587	0.78785	0.78172
39 °	0.68095	0.62953	0.77697	0.81024
40 °	0.69841	0.643	0.76586	0.83958
41 °	0.71587	0.65628	0.75452	0.86979
42 °	0.73333	0.66935	0.74295	0.90094
43 °	0.75079	0.68222	0.73115	0.93308
44 °	0.76825	0.69488	0.71913	0.96629
45 °	0.78571	0.70733	0.70688	1,00063
46 °	0.80318	0.71956	0.69443	1.0362
47 °	0.82064	0.73158	0.68176	1.07308
48 °	0.8381	0.74337	0.66888	1.11137
49 °	0.85556	0.75494	0.6558	1.15117
50 °	0.87302	0.76627	0.64252	1.1926
51 °	0.89048	0.77737	0.62904	1,2358
52 °	0.90794	0.78824	0.61537	1.28091
53 °	0.9254	0.79886	0.60152	1.32807
54 °	0.94286	0.80924	0.58748	1.37748
55 °	0.96032	0.81937	0.57326	1.42932
56 °	0.97778	0.82926	0.55887	1.48382
57 °	0.99524	0.83889	0.5443	1.54122
58 °	1.0127	0.84826	0.52957	1.60179
59 °	1.03016	0.85738	0.51468	1.66584
60 °	1.04762	0.86624	0.49964	1,73374
61 °	1.06508	0.87483	0.48444	1.80587
62 °	1.08254	0.88315	0.46909	1.8827
63 °	1.1	0.89121	0.4536	1,96476
64 °	1.11746	0.89899	0.43797	2.05265
65 °	1.13492	0.9065	0.4222	2.14707
66 °	1.15238	0.91373	0.40631	2.24884
67 °	1.16984	0.92069	0.3903	2.35894
68 °	1.1873	0.92736	0.37416	2.4785
69 °	1.20476	0.93375	0.35792	2.60887
70 °	1.22222	0.93986	0.34156	2.75169
71 °	1.23968	0.94568	0.3251	2.90892
72 °	1.25714	0.95121	0.30854	3.08299
73 °	1.2746	0.95646	0.29188	3.27686
74 °	1.29206	0.96141	0.27514	3,49427
75 °	1.30952	0.96606	0.25831	3.73993
76 °	1.32698	0.97043	0.2414	4.01992
77 °	1.34444	0.97449	0.22442	4.34219
78 °	1.36191	0.97826	0.20738	4,71734
79 °	1.37937	0.98173	0.19026	5.15984
80 °	1.39683	0.98491	0.1731	5.68998
81 °	1.41429	0.98778	0.15587	6.33709
82 °	1.43175	0.99035	0.1386	7.14523
83 °	1.44921	0.99262	0.12129	8.18379
84 °	1.46667	0.99458	0.10394	9,56868
85 °	1.48413	0.99625	0.08656	11,5092
86 °	1.50159	0.99761	0.06915	14,4259
87 °	1.51905	0.99866	0.05173	19.3069
88 °	1.53651	0.99941	0.03428	29,153
89 °	1.55397	0.99986	0.01683	59.4189
90 °	1.57143	1	0	∞

Semoga penjelasan trigonometri ini dapat bermanfaat bagi anda.

Bahan ini akan sangat berguna untuk pelbagai aplikasi dalam matematik dan fizik lanjutan.

Anda juga boleh mempelajari bahan sekolah lain di Saintif, seperti nombor perdana, penukaran unit, formula segi empat dan sebagainya.

Rujukan

• Trigonometri - Wikipedia
• Alat Matematik - Trigonometri