
31 Januari 2018 esok akan ada gerhana bulan.
Dan semua titik di Dunia berpeluang untuk menyaksikan gerhana ini.
Semua orang pasti tahu bahawa gerhana bulan berlaku kerana bumi menyekat bulan dari cahaya matahari.

Tetapi, adakah anda sudah tahu bagaimana pengiraan gerhana dilakukan?
Di sini kita akan melihat pengiraan dan simulasi lengkap untuk gerhana bulan 31 Januari esok, termasuk: Kitaran Saros, Algoritma Jean Meeus, dan Simulasi Stellarium
Kitaran Saros
Seperti peristiwa siang-malam berkala, gerhana juga berlaku secara berkala.
Gerhana matahari dan bulan mempunyai corak biasa setiap 223 bulan sinodik atau bersamaan 18 tahun, 10/11 hari, dan 8 jam.
Corak ini dipanggil kitaran Saros. Ia dinamakan oleh ahli astronomi Edmund Halley pada tahun 1886 ketika dia menyedari bahawa corak ini telah diketahui sejak zaman Babylon kuno.
Apabila dua gerhana dipisahkan oleh satu periode Saros, mereka mempunyai geometri yang hampir sama, kecuali peristiwa gerhana itu bergeser 120 darjah bujur bumi.

Kumpulan Saros Cycle gerhana secara bersiri yang berlangsung selama 12 hingga 13 abad.
Setiap siri dimulakan dengan gerhana separa di dekat tiang, dan kemudian bergerak perlahan ke tiang yang lain sehingga gambar gerhana berakhir - kemudian memulakan kitaran Saros yang lain dengan ciri-ciri gerhana baru.
Gerhana pada 31 Januari 2018 mengikuti corak kitaran Saros 124 yang bermula pada 17 Ogos 1152 dan akan berakhir pada 21 Oktober 2450.

Walaupun kitaran Saros telah berkesan dalam meramalkan kapan gerhana selanjutnya akan berlaku, kitaran Saros tidak dapat mengira masa dan jalan gerhana dengan tepat.
Oleh itu, adalah perlu untuk menganalisis pengiraan gerhana lebih lanjut seperti yang dilihat dalam katalog di atas, bermula dari kolom TD of Greatest Eclipse hingga tempoh fasa yang tidak dapat diperoleh hanya berdasarkan kitaran Saros.
Pengiraan Gerhana dengan Algoritma Jean Meeus
Salah satu kaedah mudah untuk mengira gerhana adalah algoritma Jean Meeus, yang dapat memberikan hasil dengan tahap ketepatan yang sederhana tanpa memerlukan terlalu banyak pengiraan.
Baca juga: Berikut adalah tahap-tahap gerhana bulan, anda tahu apa?Prosesnya sebenarnya agak panjang, tetapi ini hanyalah pengiraan formula gerhana matematik, jadi mudah diselesaikan - walaupun sukar difahami.

Ringkasnya, algoritma Jean Meeus berfungsi dengan mempermudah algoritma VSOP ( Variations Séculaires des Orbites Planétaires ) yang berdasarkan pergerakan planet di sekitar Matahari.
Berikut adalah algoritma Jean Meeus untuk mengira gerhana bulan:

(c) Yulia Triwahyuni, Universiti Gunadarma
Anda boleh membaca pengiraan manual terperinci di sini
Faham?
Saya juga tidak memahami perinciannya.
Tetapi jangan risau, Pak Rinto Anugraha dari UGM telah membuat fail Excel untuk algoritma Jean Meeus untuk mengira gerhana ini secara automatik.
Anda boleh memuat turun fail di sini.
Seterusnya saya akan menunjukkan kepada anda cara melakukan pengiraan gerhana bulan pada 31 Januari 2018
- Masukkan tarikh bulan dan tahun di B12, B13, B14.
- Kemudian pada B16, tulis semula nombor yang tertera di B15 (Jika gerhana matahari dimasukkan B14)

Itu sahaja yang anda masukkan. Algoritma Jean Meeus yang telah disertakan dalam fail excel ini akan melakukan pengiraan secara automatik.
Akibatnya,

Anda dapat melihat pengiraan terperinci di bahagian bawah fail excel.
Hasil pengiraan dengan algoritma Jean Meeus mempunyai tahap ketepatan yang sederhana, mari kita bandingkan hasilnya dengan data ketepatan tinggi dari pengiraan gerhana NASA.

Perbandingannya:

Perbezaannya hanya dalam jarak satu minit.
Algoritma Jean Meeus juga dapat digunakan untuk menguji sama ada kawasan tertentu dipengaruhi oleh gerhana atau tidak. Pengiraan ini melibatkan memahami bentuk bumi sfera 3 dimensi.
Anda boleh membaca perincian dan contoh cara menggunakannya dalam mekanik benda langit halaman 140 - 147 (jika anda meletakkannya di sini, ia akan sangat panjang)
Simulasi Gerhana dengan Stellarium
Pengiraan gerhana yang kompleks dan sukar difahami di atas dapat dibuat menarik dalam bentuk grafik simulasi, salah satunya adalah dengan Stellarium.
Baca juga: Salah satu kelebihan misi ke Bulan adalah mempelajari BumiStellarium adalah perisian yang menggunakan model matematik untuk mengira dan mensimulasikan pergerakan benda langit.
Anda hanya perlu memasukkan set lokasi dan masa pemerhatian, maka Stellarium akan mengira dan memaparkan cakerawala mengikut model matematik dalam aplikasi.
Bagaimana nak guna?
Mari bersama-sama mencuba gerhana bulan pada 31 Januari 2018 esok.
1. Muat turun dan kemudian buka aplikasi Stellarium
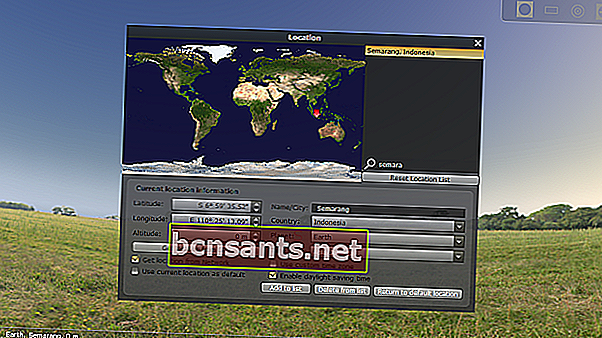
2. Tekan F6 untuk memasuki lokasi anda. Di sini saya menggunakan Semarang-World.
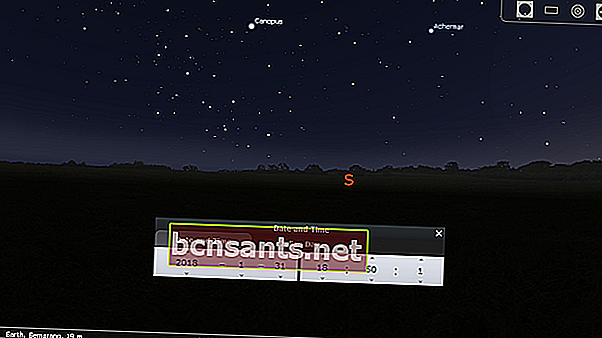
3. Tekan F5 kemudian masukkan tarikh dan masa pemerhatian
4. Tekan F3 dan masukkan perkataan "Bulan" (Jika bahasa itu Dunia Bulan), kemudian masukkan
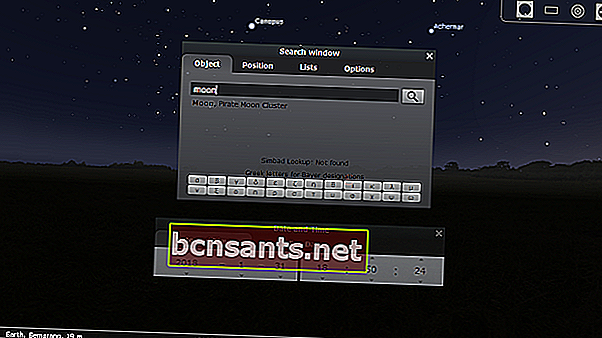
Stellarium secara automatik akan mengarahkan anda ke bulan. Zum masuk untuk melihat yang lebih jelas.

Maka anda hanya perlu bermain-main dengan masa untuk memerhatikan gerhananya.

Oleh itu, pengiraan gerhana dan simulasi gerhana bulan untuk 31 Januari 2018 esok.
Semoga dapat difahami dengan baik.
Dan mudah-mudahan kita dapat melihat gerhana bulan ini yang berada dalam bahaya tidak dapat dilihat kerana musim hujan.
Adakah Bumi rata? Masih keliru dengan bentuk sebenar Bumi?
Kami baru sahaja menyelesaikan sebuah buku yang bertajuk Membetulkan Kesalahpahaman Bumi yang Datar.

Buku ini membincangkan bentuk Bumi dengan lengkap dan jelas. Bukan hanya andaian atau pendapat.
Buku ini membincangkan kajian sains dari perspektif sejarah, konseptual, dan teknikal mengenai topik-topik yang disalahpahami oleh anting-anting. Dengan cara ini pemahaman yang komprehensif akan diperoleh.
Untuk mendapatkan buku ini, sila klik di sini secara langsung.
Rujukan:
- Buku Mekanik Celestial - Rinto Anugraha
- Ilmu Hisab - Rinto Anugraha
- Gerhana Bulan Total 2018 31 Jan - NASA
- Gerhana dan The Saros
- Pelaksanaan Algoritma Jean Meeus di Web - Yulia Triwahyuni
